数学マナぶと見えるカナ?[追記あり]
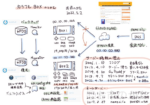
9月21日18:00−20:00で、明治大学駿河台校舎アカデミーコモン3階にある、アカデミーホールで、数検財団 主催の数学マナぶと見えるカナ? マナ★カナ×芳沢光男(よしざわ みつお)に行ってきました。1000人入れるホールに、500人くらい入っていたようです。ちなみに、一版の場合の入場料は1,000円でした。
最初は、マナカナ目当てだったのですが、実際に行ってみると、本題の数学の話の方が面白かったです。茉奈ちゃんと佳奈ちゃんも、話を盛り上げようと頑張っていたけれど、その必要がないくらいに面白かったです。茉奈ちゃんの話は、ちょっと滑り気味でした(ゴメンナサイ)。でも、それが茉奈ちゃんぽくって良いのですよね。佳奈ちゃんは、フォローに回っていました。二人を見ていると、佳奈ちゃんの方が、頭の回転が速いかなーという感じでした。
女性(女子)に数学嫌いが多いのは、日常の物として感じられないからだそうです。芳沢教授の話によると、女子は、身近な事、役に立つ物が好きだそうです。今回は、そんな観点から話が進んで行きました。
- 誕生日当てクイズ
- じゃんけんの勝ち方
- 電車の走る音から、電車の時速を求める
- 鳩ノ巣原理
- ヤミ金で1円を借りるとどうなる?サラ金の金利が18%になったらどうなる?
- 2センチメートルの定規の長さを100回倍にしたら、どんな長さになる?
- あみだくじの解法
- 富士山は日本のどこまで見える? (東京に富士見という地名が多い訳)
- 3と言う数字のマジック(円周率は、3と3.14のどちらが良い?)
誕生日当てクイズは、ある計算の後に出た数字から、その人の誕生日を当てると言う物です。在る計算とは、「日を10倍し、それに月を足す。その数字を2倍する。その数字に、さらに月を足す」と言う物です。この計算をすると、月×3+日×20をやっている事になります。この式で出る値は、月日と一対一で必ず対応し、重なる事が無いそうです。日を20倍していると言う事は、月の12月よりも大きくて、逆算しやすい数を選んでいるのだと思います。ただ、月を3倍した結果を逆算する方法が今一つわかりません。1月と11月、2月と12月は、どうやって区別しているのでしょう?
じゃんけんの勝ち方は、統計から導き出した、人間心理を元にしています。1万回以上の実験データを元に、作り上げたそうです。実際、帰宅してから子供相手に試したところ、かなりの確率で勝つ事が出来ました。
電車のレールは、25メートル毎に継ぎ目があるそうです。なので、電車のガタンゴトンという音の間隔がわかれば、電車の時速を求める事が出来ます。毎秒ガンゴトンと言う音がしていたとすると、電車の早さは秒速25メートルと言う事になります。これを時速に直すと90キロメートルになります。
鳩ノ巣原理というのは、鳩ノ巣が三つあって、4羽の鳩がいた時、巣のどれか一つには必ず歯とが2羽入る事になると言う話です。例えば、全校生徒400人だとすると、ある人とある人は必ず同じ誕生日になっている場合があると言う事が言えます。その応用として、誕生日が同じ、生まれた時間(時、分)が同じ、都道府県が同じ、血液型が同じ人は、日本にいるはずとの事です。この組み合わせは、366×24×60×47×4=99,083,520になります。1億よりも少し少ない数字です。日本の人口の方が多いので、必ず一緒になる組み合わせの人が出てくるはずとの事です。
マナカナは、「自分たちがその組み合わせでーす!」と言っていましたが、それは間違いだよと指摘したくなりました。私の記憶によると、茉奈ちゃんと佳奈ちゃんの出生時刻は7分違うはず(マナカナ – Wikipedia で読んだ)。なので、上記の例とはあわなーい。
ヤミ金の話は、ちょっと怖い。ヤミ金のレートには、「トイチ」「トニ」「トサ」があって、それぞれ、10日で一割の複利、二割の複利、三割の複利を表しているそうです。例えば、1万円を借りた時、10日後には利息を合わせて10,000×1.1=11,000。さらに10日後には、11,000×1.1=12,100。さらに10日後には12,100×1.1=13,310になるという事です。そこで出された問題が、1円を借りて10年間返さなかったら、いったいいくら返さなければならないか? と言うことです。どういう計算をするかと言うと、1^(3650/10)です。1,283,305,580,313,390円になります。1千兆円を超えています!
これと同じ話を小学生向きにアレンジすると、2センチメートルの定規を100回倍の長さにしたらどういう長さになるか? という問題です。計算は、2^100で出来ます。1,267,650,600,200,000,000,000,000,000,000センチメートル(計算器の関係で、有効桁上位11桁です)。これは、宇宙の大きさよりも大きい長さになるそうです。宇宙の大きさを約150億光年として、光の速度を秒速30万キロメートルで計算すると、確かにそうなります。自分の計算では14,191,200,000,000,000,000,000,000,000センチメートルとなりました。2桁定規の方が長くなります。講義では、「一桁差」と言っていたと思うので、私が計算を間違えたか、聞き違えたかも知れません。
あみだくじは、英語にもなっているらしいです。元は、放射状のくじで、阿弥陀如来に由来するとか。明治から大正にかけて、現在の形になったらしいです。(あみだくじ – Wikipedia もご覧下さい)
芳沢教授は、あみだくじの解法を開発していました。説明するのが大変なので、詳しくは書けませんが、ある特殊な図を書く事で、あみだくじの上下を任意につなぐ線を仕込む事が出来ます。よくぞ、開発したなぁと言う感じでした。
地球の直径を6,400キロメートル、富士山の高さを約4キロメートルとして、ピタゴラスの定理(三平方の定理)を使って計算すると、直径約230キロメートルの範囲が富士山を見える限界になります。東京から富士山の距離が、直線距離で約100キロメートルなので、東京に「富士見」という地名があるのは、妥当と言う事でした。
「3」と言う数字は、物事を理解するのに、非常に重要な数字だと、芳沢教授は熱く語っていました。例えば、二本しかないあみだくじを説明するよりも三本で出来たあみだくじを説明した方がわかりやすい、ドミノ原理を2個のドミノで説明するよりも3個のドミノで説明する方がわかりやすい、箱ティッシュの構造を2枚のティッシュで説明するよりも3枚のティッシュで説明する方がわかりやすいと言う事でした。アクセサリー(指輪)の3連リングの構造も、三つのリングから出来ているから面白くなっているとの事でした。
同様に、かけ算を理解するのに、3桁のかけ算を小学生にきちんと教える必要があると力説していました。今の学習指導要項では、2桁×2桁のかけ算までしか教えない事になっているそうです。そうなると、309×801とか、間に「0」の入った数字のかけ算を理解する事が出来なくて、困るだろうと言う話でした。なるほどと思いました。
そこで、円周率が3が良いのか3.14が良いのかと言う話になります。円周率が一時期3になってしまったのは、かけ算の学習指導要項の制限から来ているそうです。例えば、半径4センチメートルの円の面積を求める時、4×4×πとなります。つまり、16×π。ここでπを3.14としてしまうと、2桁×3桁のかけ算となってしまい、学習指導要項の制限を超えてしまいます。そこで、円周率を3にしたとか…。
ただ、円周率がどこから来ているかを考えると、「3」という数字はあながち悪くは無いとの事でした。円周率は、円周の長さは直径の何倍かを表す数字です。直径の3倍の紐を、円筒に巻き付けてみると、大体合うので、円周率の概念を教える時には使っても良い数字だと話していました。
★芳沢教授の本心は、学習指導要項で3桁×3桁のかけ算を教える事にして、円周率も3.14を使えるようにするという所にある事を、明記しておきます。
文章が長くなりました。すみません。これが、私がメモして理解した内容のほとんどです。最後に書いておきたいのは、数学(mathematic)の語源は、ギリシア語の「マテマ」(考える)という所から来ているという事です。これは、数検財団のタカダさんという方が最初に話していました。
講演の終わりに、茉奈 佳奈のミニライブがありました。講義の時とは衣装を替えての出演です。手拍子に合わせて「Fighting Girl」を歌って踊っていました。
(追記)誕生日当てクイズでは、マナカナは本当の誕生日ではなく架空の誕生日を使っていました(公正さのため)。佳奈ちゃんは9月19日、つまり
Fighting Girlの発売日を選ぶと言う、素晴らしいアイデアでした。ちなみに茉奈ちゃんは12月24日を選んでいました。
(追記 2014-07-17 21:39)
この講演で話されていた、「じゃんけんの勝ち方」は、次の通りです。
- 数学マナぶと見えるカナ? でのジャンケン必勝法 : プラスα空間 (2014年7月17日)